 Similar to the concept of Reliability computation introduced in post [003], we also would like to support the computation of system Availability with the model blocks. However, before talking about the availability arithmetics, again we have to clarify its meaning.
Similar to the concept of Reliability computation introduced in post [003], we also would like to support the computation of system Availability with the model blocks. However, before talking about the availability arithmetics, again we have to clarify its meaning.
So what is system availability? – Basically, a system can be “up” and operating, i.e. providing the required service, or “down” and non-operating, i.e. not providing the service. Being in downtime can be planned (e.g. scheduled maintenance) or unplanned (e.g. irregular failure of system parts). Dependent on the required work effort, the need and delivery time of spare parts, the qualification of the repair and maintenance team etc. it takes more or less time to repair the system and get it back into the desired “Up”-mode.
While Reliability is used to express, how probable it is that a certain desired functionality of a system fails within a given period of time, the feature of Availability quantifies the operating time within such a period. Simply put, Wikipedia summarizes Availability being “the proportion of time a system is in a functioning condition”. (If interested, please look up more explanations there.)
Besides the already mentioned MTBF, important additional calculation symbols in this context are:
- A: the symbol denoting the Availability of the respective part, item or service with theoretical values between 0 and 1, but practically usually being close to one, e.g. in high availability systems the magic “five nines” like 0.99999 or in percent this value is 99.999%, meaning 5 minutes per year (!);
- N: the symbol denoting the Non-Availability of the respective part, item or service and the complement to A, i.e. the sum of A and N is always 1;
- MTTR: the symbol denoting the Mean Time To Repair, the time needed to repair the system and get it back to service. To be correct, this time is not only needed for repair, but often is used to represent the complete downtime period, including fault detection and reporting, parts ordering (and delays), assembling, testing, start-up etc.
With these variables and stochastical parameters, the basic equations to compute the availability of a system item is:
A = MTBF / (MTBF + MTTR).
Although this maybe looks like a quite familiar equation, it is important to have a clear picture, to what these quantities really relate. Ok, MTBF and MTTR are kind of statistical parameters that have been estimated or gathered from the field and clearly can be associated to individual components. But with respect to A, we referred to certain services or functions of an item, that shall be available.
As long as we talk about system items providing only one single service, this distinction between components and their provided functions might appear artificial and not be so obvious: we can clearly observe it being Up or Down and there is a 1:1-mapping between the hardware and the functionality.
But as soon as we consider hierarchical systems or sub-systems that provide more than one single service or function, it is important to have proper and separated variable slots for the availability of system components and system functions, according to the orthogonal view we introduced earlier.
In terms of building-blocks of the SmartRAM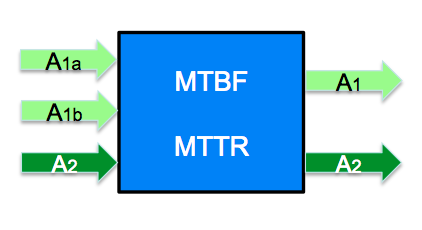 S-library in the “Availability layer” we need to provide MTBF and MTTR parameter slots only once for each component. However, concerning availability, variable slots have to be provided for each interacting service, the outgoing and the incoming ones, as illustrated in the picture. Thanks to the modular port-concept of Modelica, extending the already existing interfaces – or ports – by an additional variable for A is a matter of just one single model statement.
S-library in the “Availability layer” we need to provide MTBF and MTTR parameter slots only once for each component. However, concerning availability, variable slots have to be provided for each interacting service, the outgoing and the incoming ones, as illustrated in the picture. Thanks to the modular port-concept of Modelica, extending the already existing interfaces – or ports – by an additional variable for A is a matter of just one single model statement.
This were some basic thoughts about the required variable slots. Adding also the required arithmetics to the existing model classes and demonstrating it along the emergency power system that we used in the risk assessment example will be topic of post [007] .
 The Idea
The Idea