 The description of the last post [007] showed, how we added related quantities and arithmetics to compute availability and non-availability for individual items. This extension made them smarter and also added some “decoration” to display the parameter values.
The description of the last post [007] showed, how we added related quantities and arithmetics to compute availability and non-availability for individual items. This extension made them smarter and also added some “decoration” to display the parameter values.
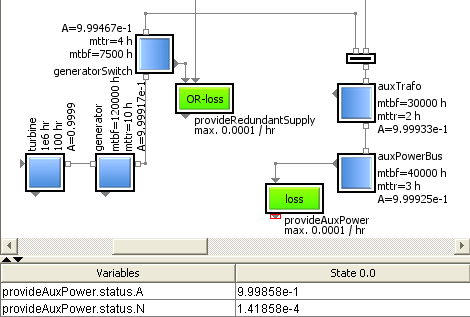
Today’s video post guides us from item level back up to system level. At the end of the day, it is the availability of a system – or better: of certain system functions – that we are interested in.
Simply by using the amended versions of the original item classes allowed it to extend the benefit of the existing system model – here in the example of the power supply system – without actually having to touch and modify it in any way. The topology remains the same as already known and graphically specified before.
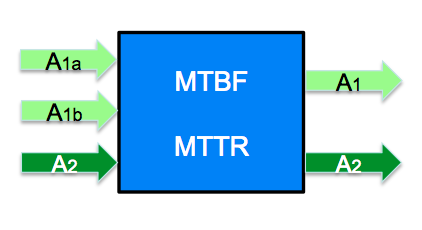
The idea is, that the individual topological context of an individual item not only determines its functionality, but also the computation of the availability of a service that this item shall provide. That means, not only its own “standalone” properties of the relevant parameters – like MTBF and MTTR as shown in post [007] – determine the service availability, but also its individual supplies have to be taken into account.
According to the local dependencies of the individual item the behavior description of its unique category automatically provides the correct arithmetics to compute this availability value. That makes it very easy to compute the availability of a system, since the computation equation is assembled automatically, just by graphically connecting the various outputs and inputs of the used items – independent if they represent real hardware components, process steps or e.g. logistical activities.
Having direct and interactive access to all relevant parameters allows to easily modify values of Mean Time Between Failures MTBF or Mean Time To Repair MTTR of any item. Just by doing a system simulation it immediately becomes clear, if these modifications help to come closer to the target number – like five nines – or also the MTBF or MTTR requirements of other items have to be tightened.
So using a graphical hierarchical system model to iteratively find out optimal target values for the items or item categories – including the feature to save and load scenarios – adds a great flexibility to the process of availability management or specification. In a later post we plan to support this process even more by considering also criteria like cost or time to get a better idea of the performance of designated assembly architectures.
In this example we assumed that the parameters MTBF and MTTR – as some of the main drivers of item availability – were given. But they are just some statistical values and depend on other properties as well. How the target function availability of a system really is affected in case a certain item is down, will probably be the topic of post [009].
For the time being, feel free to get in contact with us. 
 Here we intend to write in a sporadic manner about the development of the library.
Here we intend to write in a sporadic manner about the development of the library. The Idea
The Idea